Bilangan Bulat, FPB dan KPK SD kelas 6 dan SMP Kelas 7 K-13
Bilangan Bulat merupakan bilangan yang terdiri atas bilangan bulat negatif, nol, dan bilangan bulat positif. Himpunan bilangan bulat dinotasikan dengan B = {…,-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, …}. Pada garis bilangan, bilangan bulat digambarkan sebagai berikut.
Mari kita lihat gambar di bawah ini :
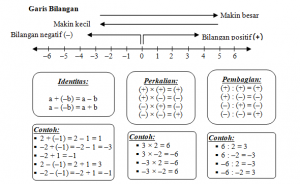
Dari gambar dapat dilihat bahwa semakin kekiri (sampai melewati dibawah angka o) maka bilangan akan semakin kecil begitu juga sebaliknya.
Dari gambar ini dapat dilihat bagaimana sifat bulat lengkap dengan contohnya, seperti :
- -3 + 5 = 2
- -3 – 5 = -8
- 3 + -5 = -2
- 2 x (-9) = -18
- (-9) : 3 = -2
- -2 : -1 = 2
Sifat-Sifat Operasi Hitung Campuran Bilangan Bulat
- Operasi penjumlahan (+) dan pengurangan (–) sama kuat, artinya operasi yang terletak di sebelah kiri dikerjakan terlebih dahulu.
- Operasi perkalian (´) dan pembagian (:) sama kuat, artinya operasi yang terletak di sebelah kiri dikerjakan terlebih dahulu.
- Operasi perkalian (´) dan pembagian (:) lebih kuat daripada operasi penjumlahan (+) dan pengurangan (–), artinya operasi perkalian (´) dan pembagian (:) dikerjakan terlebih dahulu daripada operasi penjumlahan (+) dan pengurangan (–).
Contoh Soal:
- Hasil dari (–12) : 3 + 8 ´ (–5) adalah…
Penyelesaian:
(–12) : 3 + 8 ´ (–5) = –4 + (–40)= –44
- Hasil dari -4 + 10 : 2 ´ (-5) adalah…
Penyelesaian:
-4 + 10 : 2 ´ (-5) = -4 + 5 ´ (-5)
= -4 – 25
= -29
- Suhu tempat A adalah 100 C di bawah nol, suhu tempat B adalah 200C di atas nol, dan suhu tempat C adalah tepat di antara suhu tempat A dan tempat B. Suhu tempat C adalah…
Penyelesaian:
100 di bawah nol diartikan – 100, sedangkan 200 di atas nol diartikan + 200.
Selisih antara – 100 dengan + 200 adalah 300, karena tempat C di antara tempat A dan B, maka: 300 : 2 = 150. Suhu tempat C adalah –100 + 150 = 50.
- Dalam kompetisi Matematika, setiap jawaban benar diberi skor 3, jawaban salah diberi skor -1, dan jika tidak menjawab diberi skor 0.
Dari 40 soal yang diujikan, Dedi menjawab 31 soal, yang 28 soal di antaranya dijawab benar.Skor yang diperoleh Dedi adalah…
Penyelesaian:
Tidak dijawab = 40 – 31 = 9 soal
Salah = 31 – 28 = 3 soal
28 soal benar, skornya adalah 28 × 3 = 84.
3 soal salah, skornya adalah 3 × (–1) = –
9 soal tidak dijawab, skornya 9 × 0 = 0
Skor yang diperoleh Dedi adalah 84 + (–3) + 0 = 81.
- Lebih besar manakah 766.876 dengan 876.765 ?
Penyelesaian :
Nilai tempat 7 pada 766.876 adalah ratusan ribu demikian pula nilai tempat 8 pada 876.765 adalah ratusan ribu. Karena sama – sama ratusan ribu, maka lihat angka penyusunnya, karena angka penyusun ratusan ribu 8 lebih besar dari angka penyusun ratusan ribu 7, maka bilangan 876.765 lebih besar dari bilangan 766.876.
- Terdapat bilangan yang dinyatakan ab5.def dan ab7.254, dengan a,b,d,e,f adalah angka penyusun bilangan. Lebih besar manakah antara ab5.def dengan ab7.254 ?
Penyelesaian :
Karena kedua bilangan angka penyusun a dan b memiliki nilai tempat sama, maka lihat nilai tempat ribuannya. Karena nilai tempat 5 memiliki nilai bilangan lebih kecil dari nilai tempat 7, maka bilangan ab5.def lebih kecil dari ab7.254.
Kesimpulan Sifat Bilangan Bulat
Untuk mengingat kembali mengenai Operasi Hitung silahkan di lihat slide di bawah ini (gunakan scroll atas-bawah untuk melihat 😉
Silahkan amati video di bawah ini :
FPB dan KPK
Menentukan Faktor Persekutuan Terbesar (FPB)
Ada 2 cara menentukan FPB:
Cara I
- Menentukan faktorisasi prima dari bilangan-bilangan itu
- Mengambil faktor yang sama dari bilangan-bilangan itu
- Jika faktor yang sama pangkatnya berbeda, ambillah faktor yang pangkatnya terkecil
Contoh Soal:
Tentukan FPB dari 12 dan 18!
Penyelesaian :
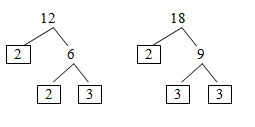 Faktorisasi prima dari 12 adalah 12 = 2 × 2 × 3 = 22 × 3
Faktorisasi prima dari 12 adalah 12 = 2 × 2 × 3 = 22 × 3
Faktorisasi prima dari 18 adalah 18 = 2 × 3 × 3 = 2 × 32
FPB dari 12 dan 18 adalah 2 × 3 = 6.
Cara II
Pengertian awal FPB adalah bilangan yang dapat membagi. Jadi FPB suatu bilangan adalah bilangan yang dapat membagi habis (tanpa sisa) suatu bilangan tersebut.
- Bilangan yang lebih besar dikurangi dengan bilangan yang lebih kecil terus menerus sampai hasilnya dapat membagi habis kedua bilangan.
- Jika hasil yang kita temukan belum bisa membagi habis keduanya, proses masih harus dilanjutkan sampai menemukan bilangan yang bisa membagi habis keduanya.
Contoh Soal:
- FPB dari 24 dan 40
40 – 24 =16
16 belum bisa membagi 40 dan 24, maka proses dilanjutkan dengan mengurangi bilangan yang lebih kecil dari 40 dan 24 dengan hasilnya.
24 – 16 = 8
8 bisa membagi habis 40 dan 24
Jadi FPB dari 40 dan 24 adalah 8
- FPB dari 64 dan 40
64 – 40 = 24
24 belum bisa membagi 64 dan 40, proses dilanjutkan
40 – 24 = 16
16 belum bisa membagi 64 dan 40, proses dilanjutkan
24 – 16 = 8
8 sudah bsia membagi habis bilangan 64 dan 40
Jadi FPB dari 64 dan 40 adalah 8
Menentukan Kelipatan Persekutuan Terkecil (KPK)
Ada 2 cara menentukan KPK:
Cara I
- Tentukan faktorisasi prima dari bilangan-bilangan tersebut.
- Ambil semua faktor yang sama atau tidak sama dari bilangan-bilangan tersebut.
- Jika faktor yang sama memiliki pangkat berbeda, ambillah faktor yang pangkatnya terbesar.
Contoh Soal:
Tentukan KPK dari 12 dan 18!
Penyelesaian:
 Faktorisasi prima dari 12 adalah 12 = 2 × 2 × 3 = 22 ×3.
Faktorisasi prima dari 12 adalah 12 = 2 × 2 × 3 = 22 ×3.
Faktorisasi prima dari 18 adalah 18 = 2 × 3 × 3 = 2 × 32.
KPK dari 12 dan 18 adalah 22 × 32 = 4 × 9 = 36.
Cara II
Untuk menentukan KPK suatu bilangan, dasarnya adalah FPB dari bilangan tersebut, jadi kita harus lebih dulu mencari FPB nya.
Contoh Soal:
- Tentukan KPK dari 24 dan 18
FPB dari 24 dan 18 adalah 6
24 : 6 = 4, dan 18 : 6 = 3
KPKn ya 6 × (4 × 3) = 6 × 12 = 72
Jadi KPK dari 24 dan 18 adalah 72
- KPK dari 75 dan 50
FPB dari 75 dan 50 adalah 25
75 : 25 = 3, dan 50 : 25 = 2
KPKnya 25 × (3 × 2) = 25 × 6 = 150
Jadi KPK dari 75 dan 50 adalah 150
Untuk cara menentukan faktorisasi prima dengan pohon faktor silahkan lihat video di bawah ini :
Latihan Pertama Bilangan Bulat
Tanya jawab dan diskusi materi Bilangan Bulat serta FPB dan KPK
Teman-teman bisa bertanya tentang materi ini melalui :
- Kolom bertanya (Kolom komentar)
- Sosial Media khusus Senopati Center (gratis) : https://www.senopatieducationcenter.com/secsocial
- Halaman Facebook Senopati Center : https://web.facebook.com/senopatieducationcenter
- Masih kurang? Ikuti Coba gratis kelas online tatap muka kami (Live Online Class) melalui zoom meeting yang dipadu dengan animasi menarik, latihan dan try out online melalui website ini serta fasilitas menarik lainnya.
- Takut sinyal bermasalah? Jangan khawatir, setiap pertemuan akan kami rekam dan kirimkan ke kalian secara berkala, tanya jawab dari materi gersebut bisa kalian tanyakan melalui WhatsApp Online kami (Live Chat).
- Takut quota habis? Aktifkan paket belajar online sesuai dengan provider android atau apple kalian.
- Bagaimana cara mengikuti Cobe kelas online (Live Online Class) kami? Silahkan isi form pendaftaran pada link yang ada di kolom attachment (lampiran).
- Masih banyak pertanyaan yang mau ditanyakan? Silahkan chat kami melalui WhatsApp online Senopati Center yang ada di website ini (maaf, kami hanya melayani Chat WhatsApp).
Setelah memahami materi ini maka kalian dapat menjawab soal-soal latihan essay pada link yang ada di kolom attachment (lampiran). Selamat mengerjakan!

